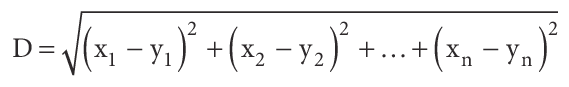Part 1
When I was studying AI at the university, I remember this interesting problem called The Travelling Salesman or TSP which we were given to solve in one of the assignments, it was so fun to me that I decided to write this article about it.
Imagine a business man or salesman (or you) wanted to travel to say 4 different cities around the world and come back home, but you wanted to know in which order of travelling from one city to another gives you the shortest route (maybe to save fuel if going by car). In this case, since we’re dealing with 4 cities total, the best way of knowing for sure would be to calculate literally each possible path combination and then measure which one gives the shortest total distance in kilometers.
| City # | x coordinate | y coordinate |
| 1. | 37 | 52 |
| 2. | 49 | 49 |
| 3. | 52 | 64 |
| 4. | 20 | 26 |
The cities are plotted on a graph using the x, y coordinates above.

Factorials and Permutations
In order to calculate all the possible variations of the path to travel, we need to get all the cities arranged in all of the possible orders. In mathematics, factorials are used to calculate the total number of possible unique combinations of distinct sequences made from a list of unique objects. The formula for factorial calculation is the following.
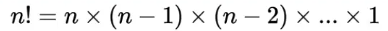
Where n is the number of cities in our case, hence it would resolve as follows. The ! symbol followed by he digit indicates the factorial operation.
4! = 4 * 3 * 2 * 1 = 24
This means that we need to figure out 24 different combinations of paths to travel in total, but how do we do this? Well.. we can either do that manually or we can use some math or code instead using what is called a permutation. So by implementing a permutation function in C# in my case, I will be able to get all the 24 possible unique sequences of the cities. The code for this function can be found [here] (which I ripped from an example I found online).

When running the permutation for the 4 cities with labels {1, 2, 3, 4}, the result below is produced.
|
|
|
I had some fun with JavaScript illustrating all 24 permutations in an animation. You can have a look [here].
Distance between 2 points
Now that we figured out all the possible unique sequences of the paths we need to solve, we need to find out the total distance of the path. In order to achieve this, the distance from point to point needs to be calculated and then summed. To find the distance between two points (often referred as Euclidean Distance), we need to use the Pythagoras Theorem.
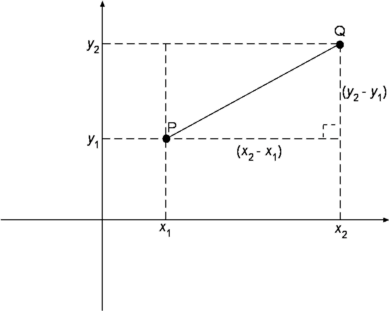
Thus if we define any two points as P and Q, we solve the Euclidean distance as follows.
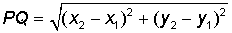
In C# code this translates to something like the following.
double dist = (double) Math.sqrt(
Math.pow(city1.x - city2.x, 2) +
Math.pow(city1.y - city2.y, 2));The code [here] shows how we calculate the path for each route. Below is the generated results in console.
route: 4, 1, 2, 3, 4, dist: 108.41
route: 4, 2, 1, 3, 4, dist: 118.27
route: 4, 3, 1, 2, 4, dist: 118.27
route: 4, 3, 2, 1, 4, dist: 108.41
route: 4, 1, 3, 2, 4, dist: 102.58
route: 4, 2, 3, 1, 4, dist: 102.58
route: 3, 4, 2, 1, 3, dist: 118.27
route: 3, 4, 1, 2, 3, dist: 108.41
route: 2, 4, 1, 3, 2, dist: 102.58
route: 1, 4, 2, 3, 1, dist: 102.58
route: 2, 4, 3, 1, 2, dist: 118.27
route: 1, 4, 3, 2, 1, dist: 108.41
route: 3, 1, 4, 2, 3, dist: 102.58
route: 3, 2, 4, 1, 3, dist: 102.58
route: 2, 3, 4, 1, 2, dist: 108.41
route: 1, 3, 4, 2, 1, dist: 118.27
route: 2, 1, 4, 3, 2, dist: 108.41
route: 1, 2, 4, 3, 1, dist: 118.27
route: 3, 1, 2, 4, 3, dist: 118.27
route: 3, 2, 1, 4, 3, dist: 108.41
route: 2, 3, 1, 4, 2, dist: 102.58
route: 1, 3, 2, 4, 1, dist: 102.58
route: 2, 1, 3, 4, 2, dist: 118.27
route: 1, 2, 3, 4, 1, dist: 108.41
Winner is: 4, 1, 3, 2, 4, dist: 102.58It is important to notice that when dealing with such small number of cities, it is common to have routes with the same distance. In fact, although the algorithm says that the winner route is 4, 1, 3, 2, 4 the route with sequence 1, 3, 4, 2, 1 and a few others have the same exact distance of 102.58 km. Nevertheless, this is the shortest route possible of the 24 permutations.
The Factorial Problem
So one might be thinking at this point, OK! problem solved then! brute force can calculate each possible path and we will know which is the shortest path to take. Well… yes, the truth is that if you want to know which route is the absolute shortest, then a brute force algorithm will give the most accurate answer, so why do we need AI? And the answer is the problem with factorials and number of probabilities when dealing with a larger number of cities.
When dealing with even 10 or 20 cities (which isn’t a lot if you think about it) the factorial reaches astronomical values and I’m not even exaggerating. For instance, if we’re dealing with 10 cities:
10! = 1,307,674,368,000
Yes, that is a staggering 1.3 Trillion permutations we need to find and if we had to calculate 1 permutation every 1 millisecond, it would take us over 41 years. What about 20 cities?
20! = 2,432,902,008,176,640,000
That’s 2.4 Quintillion permutations, and would take us over 77 Million years if we calculated 1 permutation every 1 millisecond. Still not convinced? What about 70 cities? Well…
70! = 1.197857167×10100
Fun fact: scientists have calculated there are between 1×1078 to 1×1082 atoms in the known, observable universe. This means that if we had write the answer of each permutation that we found on every atom in the universe, we would eventually run out of atoms with about 20% permutations left to find. Anyway! we get the idea…
These are probabilities that not even the world’s best super computers can calculate in a lifetime and therefore Artificial Intelligence can be used to find approximations of the best routes. It’s important to keep in mind that there’s no free lunch in AI and this means it’s probably impossible to ever find the absolute best path when dealing with numerous cities but despite this, some algorithms can help narrowing down the results quite well.
Nearest Neighbour
In another article which I had posted [here] the nearest neighbour algorithm was explained and put to use to find similar patterns by calculating the Euclidean distance between different digit sequences. This can also be applied to attempt resolving the TSP problem by starting at a random city, then calculating which is the nearest city next to that point by shortest distance and move to that one as the next hop in the sequence. This means that the Euclidean distance is calculated from the current city to each of the other cities at each unvisited point at every iteration until all cities are visited.
Using the code [here] I ran the NN algorithm to solve a TSP problem with 51 cities from a [file]. The results I got is the following:
{
distance: 513.610006884723,
city_order: "1, 32, 11, 38, 5, 49, 9, 50, 16, 2, 29, 21, 34, 30, 10, 39, 33, 45, 15, 44, 37, 17, 4, 18, 47, 12, 46, 51, 27, 48, 6, 14, 25, 13, 41, 19, 42, 40, 24, 23, 7, 26, 8, 31, 28, 3, 20, 35, 36, 22, 43, 1, "
}Who’s to argue with that, right? This is what the algorithm says is the most viable route using the Nearest Neighbour operation, but how can we be sure this is the best? How would the NN compare to the brute force algorithm if we had to run it for the 4 cities in the previous example?
{
distance:108.40979394514636,
city_order:"1, 2, 3, 4, 1, "
}Interesting! Although it didn’t pick the longest route, it didn’t pick the shortest either (hence 102.58) so this makes me think it’s not very efficient at finding the most optimal path on the 51 cities either.
Conclusion
In this article the Travelling Salesman Problem is introduced and brute force is used as a first attempt to find the solution. This solution works the best when dealing with a small number of cities but as the number of cities grow, the permutations grow exponentially, so much that no computer would ever be able to solve the problem in less than millions or billions of years.
For this reason, there are some interesting Artificial Intelligence algorithms often known as Heuristics which can approximate and optimise the results in a very short time. The nearest neighbour is one of the simplest of such algorithms which has been explored. In the next part of this article I will be covering other more complex and interesting algorithms of this sort which will help finding a more efficient route to solve the TSP.
Check out the brute force animation I created in JavaScript [here] if you haven’t already.
As always, stay tuned for part 2!
References
1. Pythagoras Theorem diagrams
http://mathsfirst.massey.ac.nz/Algebra/PythagorasTheorem/pythapp.htm
2. Permutations algorithm in C#
https://www.daniweb.com/programming/software-development/threads/349926/c-string-permutation#post1485682
3. N! Factorials
https://en.wikipedia.org/wiki/Factorial